Hypo-technique 1: Lego rotation principles and basic hinged Hypo-tech

The Hypo-technique formerly known as “Jumper technique” is a highly versatile technique for connecting lego sections to each other at odd angles. The beauty is that it gives you a vast range of different angles, that it can be scaled to any size, and that you can choose to make it as simple or complex as you want.

Before we can start with the Hypo-technique, however, I believe that a brief discussion of some basic (lego) rotation principles would make everything much easier.

Skip to the Hypo-technique, or the angles you can achieve with it.

Basic lego rotation

Basic 1-point rotation
To begin with the basics: Lego is a building system based on 90-degree angles, which is perfectly suited for making boxes. However, boxes tend to get boring in the long run, which is one of the reasons The Lego Company has made a range of different parts that can be used rotate sections of lego relatively to each other. The trouble with these parts is that they typically either lock the rotation at a particular angle that you may not want, or rotate more or less freely around a single point in the form of a hinge, which is rarely strong enough for larger sections, while smaller stuff like antennas will be too easily pushed out of position.

3-point rotation
Instead of relying on just one rotation-point, you can however, strengthen your construction with a triangle: Instead of having just one point that can rotate, each section is locked to the others by two fixed points.
This locked rotation does certainly have its uses because it can create a lot of interesting angles (especially the equal-sides-60-degree variant), but also a range of problems: first and foremost you end up with an ugly triangular gap that is hard to cover up, secondly most the stress from weight and gravity will be placed solely on 2-3 hinges that, thirdly, need to be placed wide apart when it come to larger constructions to avoid torsion: which will create even larger triangular gaps.

Pythagorean triangle
A special 3-point rotation technique worth noticing is the Pythagorean triangle: The beauty of this technique is that with sides of 3, 4, and 5 studs, one of the corners will be right-angled, which not only fit the overall 90-degree building system, but also let you duplicate the technique down along the line of the hypotenuse without messing up angles and distances (unlike the other triangles with different side lengths).
The trouble with the 3-4-5 is of course that you can only make angles of 36,87 or 53,13 (which is basically the same angle because 53,13=90-36,87 degrees, so I’ll only mention the smaller in the following).

It would be really nice if it was possible to vary this angle simply by changing the length of the two sides at a right angle. Unfortunately there are only a fairly limited number of combinations of sidelengths that will result in an integer hypotenuse, and they tend to grow to SHIP-size awfully fast (you can find a table a bit down this section): Any other combination will land you in a real mess if you try to connect the hinges on the hypotenuse-side and build anything on this side of the triangle:

With a lot of experimentation or serious geometric calculation you may approximate an integer hypotenuse, but this will always bend your parts to some degree which will damage them in the long run: A particularly nasty example of this is the official UCS Imperial Stardestroyer which, among many other illegal techniques, have a triangle on basic framework with a hypotenuse-side half a stud off the calculated distance, wich probably is the reason the side-panels pop off once in a while (read more about TLC's list of illegal techniques here to avoid damaging you own parts).

Personally I don’t use such techniques because I don’t want to damage my lego, because it take ages to figure out exactly how long the sides need to be in order to achieve a given angle, but mostly it’s because I’ve discovered the Hypo-technique that is not only more versatile, but also much easier:

Hinged Hypo-tech

Basically, the Hypo-technique or “mirrored Hypotenuse technique” is a 4-point rotation technique that circumvent the problems with odd-length hypotenuses by simply leaving them out!

In the last example with two hinges put together to form a triangle with sidelengths of 1, 2 and a completely unpractical hypotenuse of ~2.34 - but instead of messing around with varying side-lengths, half-plate techniques and worse, we can simply mirror the triangle and click the two sections together without any stress or damage to the parts, because the hypotenuses of the mirrored triangles will always be of equal length: and that's basically the Hypo-technique for you.

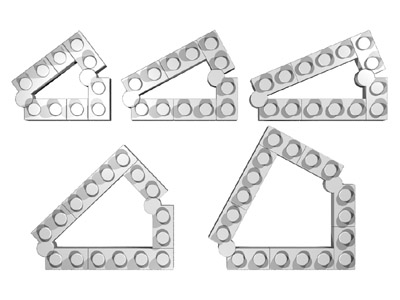Of course the two triangles put together will create a steeper angle (53,13 degrees), but by varying the sidelengths of the right-angled sides, you can just adjust it to fit your particular needs. In the examples to the right the angles are 36,87; 28,07; 22,62 and climbing again in the lower row to 43,60 and 61,73.

Examples

Here are some examples of Hypo-tech hinge-version in use:

Angled hull on an ancient spaceship by Mike Psiaki using a 3/9 Hypo-tech

An angled hull on my 78 Railgun Spider using a basic 2/5 Hypo-tech

Wings with very advanced 3-axis rotation by Bram Lambrecht using a multiplying a 2/9 Hypotech down the center line (it just work - even if you leave out some of the hinges/attachment points).

Angles achievable with integer Hypo-tech (>10 studs)

Finally, here's a list of angles you can achieve by using the Hypo-tech. The white cells along the edges is the length of the two sides next to the right angle, while the coloured cells show which angles will be achieved with a given combination.
Note that every rotation will result in two angles compared to the overall 90 degree lego grid and that I've consistently choosen the smaller one. If you need angles higher than 45 degrees such as 60 degrees, you just subtract it from 90 (90-60=30) and find the closest fit in the table below:

	1	2	3	4	5	6	7	8	9
2	36,87								40-45
3	36,87	22,62							30-40
4	28,07	36,87	16,26						20-30
5	22,62	43,60	28,07	12,68					10-20
6	18,92	36,87	36,87	22,62	10,39				0-10
7	16,26	31,89	43,60	30,51	18,92	8,78
8	14,25	28,07	41,11	36,87	25,99	16,26	7,63
9	12,68	25,06	36,87	42,08	31,89	22,62	14,25	6,73
10	11,42	22,62	33,40	43,60	36,87	28,07	20,02	12,68	6,03

You will notice that there isn't that many different angles to choose from, especially in the <10 degree range, in the next part of the tutorial we'll have a look at layered Hypo-technique: It's a little more complicated to work with, but in return you'll get 120% more options for angles using a third of the space and better possibilities to cover up gaps.
Furthermore this technique makes it easy to create strong multi-point techniques (resembling the pythagorean triangle) which will also be covered.

But until I find the time to sit down and write it, play around with the hinged version to get a better feeling for it.

-

This article was announced in this thread on CSF, where Bram Lambrecht showed us a cool assymetric version of the Hypo-technique, while Tony Haffner amazed us with an even more advanced 2-axis version rotated 45 degree horizontally!